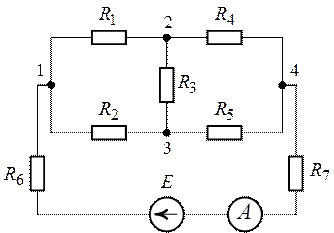
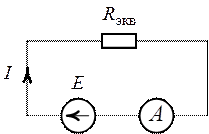
Дана электрическая схема известны эдс источников тока и сопротивление резисторов
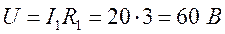
Оглавление:
Метод контурных токов.Решение задач
1 – Выбор направления действительных токов. 2 – Выбор независимых контуров и направления контурных токов в них. 3 – Определение собственных и общих сопротивлений контуров 4 – Составление уравнений и нахождение контурных токов 5 – Нахождение действительных токов Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример. Выполняем все поэтапно.
1. Произвольно выбираем направления действительных токов I1-I6.
2. Выделяем три контура, а затем указываем направление контурных токов I11,I22,I33. Мы выберем направление по часовой стрелке. 3. Определяем собственные сопротивления контуров.
Для этого складываем сопротивления в каждом контуре. R11=R1+R4+R5=10+25+30= 65 Ом R22=R2+R4+R6=15+25+35 = 75 Ом R33=R3+R5+R6=20+30+35= 85 Ом Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R4 принадлежит контуру 1 и контуру 2.
Определение токов во всех резистивных элементах и проверка полученных результатов с помощью первого или второго законов Кирхгофа
состоит из последовательно соединенных активного R и реактивного Х сопротивлений.
Требуется определить параметры R и Х, а также L или С этой цепи, используя дополнительное сопротивление R1, величина которого известна, и только амперметры или только вольтметры электромагнитной системы.
Частота f источника питания цепи известна.
Номер схемы 2; I1 = 15 A, I2 = 20 A, I = 32 A, R1 = 3 Ом, f = 450 Гц. Рис. 2.1. Решение: На основании первого закона Кирхгофа строим векторную диаграмму токов данной цепи. Произвольно проводим вектор приложенного напряжения, действующее значение которого
.
Вектор тока
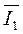
совпадает по фазе с вектором напряжения, как ток в активном сопротивлении. Из начала вектора (точка а) описываем дугу радиусом I, а из конца вектора дугу радиусом I2.
Решение задач по электротехнике (ТОЭ)
Для схемы на рисунке (стрелкой обозначим направление вдоль контура, которое будем считать условно положительным).
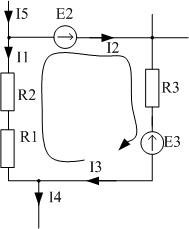
Начиная с узла, где сходятся токи I1, I3, I4 запишем все напряжения (по закону Ома): -I1⋅R1 — I1⋅R2 – в первой ветви (знак минус означает, что ток имеет направление противоположное выбранному направлению контура).
I3⋅R3 – во второй ветви (знак «плюс», направление совпадает).
Теперь запишем ЭДС: E2 — E3 (знак «минус» у E3, потому что направление ЭДС противоположно направлению контура). В соответствии с законом Кирхгофа напряжения равны ЭДС: -I1⋅R1 — I1⋅R2 + I3⋅R3 = E2 — E3. Как видите, все довольно просто.
В большинстве случаев перед студентами стоит задача рассчитать величины токов во всех ветвях, зная величины ЭДС и резисторов. Для расчета сложной, разветвленной цепи постоянного тока, например этой, найденной на просторах интернета, воспользуемся следующими действиями.
Общая электротехника и электроника
Электродвижущая сила — электрическая разность потенциалов, создаваемая источником электрической энергии (электрохимическим элементом, механическим генератором, термоэлементом, фотоэлементом и пр.). Приемники, или нагрузка, т.е. устройства, потребляющие электрический ток (электродвигатели, электролампы, электрические механизмы и т.д.).
Проводники, а также различная коммутационная аппаратура (выключатели, реле, контакторы и т.д.). Направленное движение электрических зарядов называют электрическим током.
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом. Рис. 1 Решение Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е.
от зажимов a−g: Задача 2. Для цепи (рис.
2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
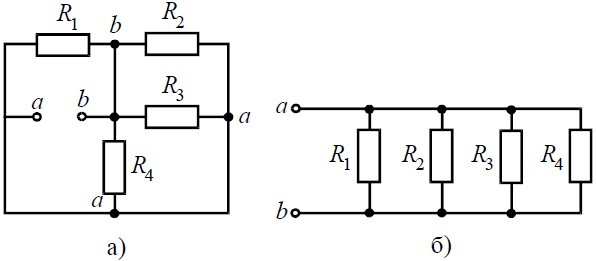
Рис. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
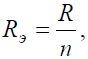
где R – величина сопротивления, Ом; n – количество параллельно соединенных сопротивлений.
Примеры решения задач на законы Кирхгофа
Аналогично с источниками ЭДС.
Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка . Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.
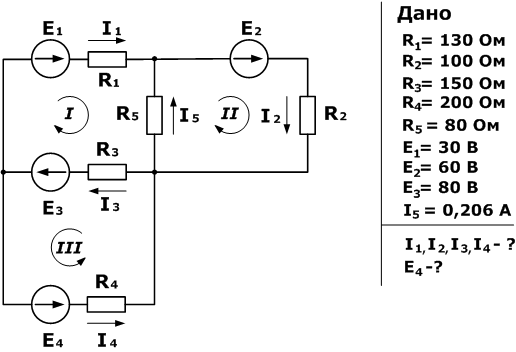
Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2 Затем составляем уравнения по второму закону для трех контуров.
Расчет сопротивления электрической цепи
Электрическая схема простейшей электрической цепи, обеспечивающей работу осветительной аппаратуры, представлена на рис.
1.1. Рис. 1.1 Все устройства и объекты, входящие в состав электрической цепи, могут быть разделены на три группы: 1) Источники электрической энергии (питания).
Общим свойством всех источников питания является преобразование какого-либо вида энергии в электрическую. Источники, в которых происходит преобразование неэлектрической энергии в электрическую, называются первичными источниками.
Вторичные источники – это такие источники, у которых и на входе, и на выходе – электрическая энергия (например, выпрямительные устройства).
2) Потребители электрической энергии. Общим свойством всех потребителей является преобразование электроэнергии в другие виды энергии (например, нагревательный прибор). Иногда потребители называют нагрузкой.
3) Вспомогательные элементы цепи: соединительные провода, коммутационная аппаратура, аппаратура защиты, измерительные приборы и т.д., без которых реальная цепь не работает.
Расчет электрических цепей
3.
В таком случае полезно найти точки с одинаковым потенциалом (например, соединенные проводами, сопротивление которых в таких задачах считают обычно пренебрежимо малым).
Затем надо перечертить схему, объединив точки с одинаковым потенциалом. Рассмотрим, например, схему участка цепи, изображенную на рисунке 61.2.
Расчет простых цепей при постоянных токах и напряжениях.
Расчет сложных цепей с помощью прямого применения законов Кирхгофа (главы 1-2 учебного пособия «Теоретические основы электротехники в примерах и задачах»), страница 2
, если
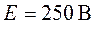
,
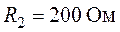
,
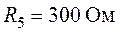
,
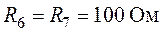
).