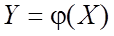
Главная - Завещание - Две независимые дискретные случайные величины х и у заданы своими

Две независимые дискретные случайные величины х и у заданы своими


Две независимые дискретные случайные величины х и у заданы своими

Пример решения


Множество всех возможных значений дискретной случайной величины с их вероятностями называется законом распределения этой случайной величины. Дискретная двумерная случайная величина (X,Y) считается заданной, если известен ее закон распределения: P(X=xi, Y=yj) = pij, i=1,2.,n, j=1,2.,m X / Y 20 30 40 50 60 11 2 0 0 0 0 16 4 6 0 0 0 21 0 3 6 2 0 26 0 0 45 8 4 31 0 0 4 6 7 36 0 0 0 0 3 События (X=xi, Y=yj) образуют полную группу событий, поэтому сумма всех вероятностей pij(i=1,2.,n, j=1,2.,m), указанных в таблице, равна 1.

1. Зависимость случайных величин X и Y. Находим ряды распределения X и Y. Пользуясь формулой ∑P(xi,yj) = pi (j=1.n), находим ряд распределения X. X 11 16 21 26 31 36 P 2 10 11 57 17 3 ∑Pi = 100 Математическое ожидание M[X]. M[x] = (11*2 + 16*10 + 21*11 + 26*57 + 31*17 + 36*3 )/100 = 25.3 Дисперсия D[X].
D[X] = (112*2 + 162*10 + 212*11 + 262*57 + 312*17 + 362*3 )/100 — 25.32 = 24.01 Среднее квадратическое отклонение σ(x).

В задачах 191–200 заданы дискретные случайные величины

193. Из имеющихся шести билетов лотереи, из которых четыре невыигрышных, наудачу вынимают по одному билету до тех пор, пока не встретится выигрышный билет. Составить закон распределения случайной величины X – числа вынутых билетов, если каждый вынутый билет обратно не возвращается.

Найти математическое ожидание и среднее квадратическое отклонение этой случайной величины.

194. Студент может сдавать экзамен не более четырех раз. Составить закон распределения случайной величины X – числа попыток сдать экзамен, если вероятность его сдачи – 0,75 и в дальнейшем возрастает на 0,1 при каждой следующей попытке. Найти дисперсию этой случайной величины. 195. Даны законы распределения двух независимых случайных величин X и Y: X – 6 Y – 3 – 1 P 0,3 0,45 0,25 0,75 0,25 Составить закон распределения случайной величины X–Y и проверить свойство дисперсии D(X –Y) = D(X) + D(Y).

Moneyprofy.ru

Известны математические ожидания и дисперсии двух независимых случайных величин X и Y : M(x)=8 , M(Y)=7 , D(X)=9 , D(Y)=6 .

Найти математическое ожидание и дисперсию случайное величины Z=9X-8Y+7 . Решение. Исходя из свойств математического ожидания: M(Z) = M(9X-8Y+7) = 9*M(X) — 8*M(Y) + M(7) = 9*8 — 8*7 + 7 = 23.

Исходя из свойств дисперсии: D(Z) = D(9X-8Y+7) = D(9X) — D(8Y) + D(7) = 9^2D(X) — 8^2D(Y) + 0 = 81*9 — 64*6 = 345 math.semestr.ru Пусть задана функция

случайного аргумента Х. Требуется найти математическое ожидание этой функции, зная закон распределения аргумента.

1. Пусть аргумент Х—дискретная случайная величина с рядом распределения

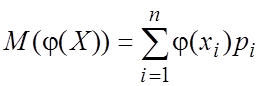
. Пример 3. Дискретная случайная величина Х задана распределением Найти математическое ожидание функции

.

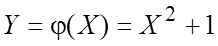
Дискретные случайные величины

Соответствие между этими значениями и их вероятностями называется законом распределения дискретной случайной величины.

Рекомендуем прочесть:  Какая стртья доется наркоманом

Как правило, это соответствие задается с помощью таблицы, в первой строке которой указывают значения $x_1,\dots ,\ x_n$, а во второй строке соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$. $\begin{array}{|c|c|} \hline X_i & x_1 & x_2 & \dots & x_n \\ \hline p_i & p_1 & p_2 & \dots & p_n \\ \hline \end{array}$ Пример 2.

Пусть случайная величина $X$ — число выпавших очков при подбрасывании игрального кубика. Такая случайная величина $X$ может принимать следующие значения $1,\ 2,\ 3,\ 4,\ 5,\ 6$. Вероятности всех этих значений равны $1/6$.

Тогда закон распределения вероятностей случайной величины $X$: $\begin{array}{|c|c|} \hline 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\ \hline \end{array}$ Замечание. Поскольку в законе распределения дискретной случайной величины $X$ события $1,\ 2,\ \dots ,\ 6$ образуют полную группу событий, то в сумме вероятности должны быть равны единице, то есть $\sum{p_i}=1$.
Математическое ожидание случайной величины задает ее «центральное» значение.

Функции одного и двух дискретных случайных аргументов. Совместное распределение двух дискретных случайных величин

При вычислении вероятностей pi используются правила вычисления вероятностей произведения независимых событий и суммы несовместных событий.

Ряд распределения СВ Z имеет вид: zi –1 pi 0,12 0,38 0,38 0,12 Контроль:

Аналогично находим ряд распределения случайной величины W = X × Y.

Найдем wij = xiyj: w11 = 1 × 1 = 1, w12 = 1 × 2 = 2, w21 = 2 × 1 = 2, w22 = 2 × 2 = 4, w31 = 3 × 1 = 3, w32 = 3 × 2 = 6. Тогда w1 = w11 = 1, w2 = w21 = w12 = 2, w3 = w31 = 3, w4 = w22 = 4, w5 = w32 = 6. p1 = P(W = 1) = P(X = 1, Y = 1) = P(X = 1) × (Y = 1) = 0,3 × 0,6 = 0,18; p2 = P(W = 2) = P((X = 1, Y = 2) + (X = 2, Y = 1)) = = P(X = 1) × P(Y = 2) + P(X = 2) × P(Y = 1) = 0,3 × 0,4 + 0,5× 0,6 = 0,42; p3 = P(W = 3) = P(X = 3, Y = 1) = P(X = 3) × P(Y = 1) = 0,2× 0,6 = 0,12; p4 = P(W = 4) = P(X = 2, Y = 2) = P(X =

Системы случайных величин


Инструкция.

Укажите размерность матрицы распределения вероятностей (количество строк и столбцов) и ее вид.

Полученное решение сохраняется в файле Word. Размерность матрицы распределения вероятностей 2345678910 x 2345678910 Y по вертикали, X — по горизонтали Y/Xx1x2xp y1p1p2pn ymp1mp2mpnm Y по горизонтали, X — по вертикали X/Yy1y2yp x1p1p2pn xmp1mp2mpnm Пример №1.

Двумерная дискретная случайная величина имеет таблицу распределения: Y/X 1 2 3 4 10 0 0,11 0,12 0,03 20 0 0,13 0,09 0,02 30 0,02 0,11 0,08 0,01 40 0,03 0,11 0,05 q Найти величину q и коэффициент корреляции этой случайной величины.

Рекомендуем прочесть:  Оброзец заявление на алименты если у отвечика есть еще дети

Решение. Величину q найдем из условия Σpij = 1 Σpij = 0,02 + 0,03 + 0,11 + … + 0,03 + 0,02 + 0,01 + q = 1 0.91+q = 1.

Откуда q = 0.09 Находим ряды распределения X и Y.

Пользуясь формулой ∑P(xi,yj) = pi (j=1.n), находим ряд распределения X. X 10 20 30 40 P 0.26 0.24 0.22

Понятие случайной величины. Закон распределения случайной величины

Поэтому изменение скоростей молекул газов носит случайных характер.

Действия над случайными величинами.
Приведенные примеры показывают, что со случайными величинами приходится иметь дело в самых разнообразных областях науки и техники. В каждом из приведенных примеров мы имеем дело с величинами, характеризующими исследуемое явление. Каждая из этих величин случайным образом принимает различные значения, т.е.

заранее сказать, какое значение примет величина, нельзя, так как она от испытания к испытанию меняется случайным образом. Определение1. Случайной величиной называется переменная, которая в результате испытания (опыта) в зависимости от случая принимает одно из совокупности возможных своих значений, причем заранее неизвестно, какое именно.

Иначе, случайная переменная величина представляет собой некоторую числовую функцию, которая определена на пространстве элементарных событий Ω. Эта функция ставит в соответствие каждому элементарному событию ω некоторое число.

Программа, методические указания к самостоятельному изучению дисциплины и контрольные задания для студентов заочной формы обучения Хабаровск 2007

В магазине куплено 3 электроприбора: чайник, утюг и пылесос. Вероятность выхода из строя в течение гарантийного срока для каждого из них соответственно равны р1=0,05, р2=0,1, р3 = 0,2.

Составить закон распределения случайной величины Х – числа приборов, вышедших из строя в течение гарантийного срока. Решение: Х – число приборов, вышедших из строя, имеет следующие возможные значения: х1=0 – все три прибора не выйдут из строя в течение гарантийного срока; х2=1 – один прибор выйдет из строя; х3=2 – два прибора выйдут из строя; х4=3 – три прибора выйдут из строя. Найдём соответствующие этим значениям вероятности.

По условию вероятности выхода из строя приборов равны: р1=0,05; р2=0,1; р3=0,2, тогда вероятности того, что приборы будут рабочими в течение гарантийного срока равны: q1 = 1 – p1 = 1 – 0,05 = 0,95; q2 = 1 — p2 = 1 – 0,1 = 0,9; q3 = 1 – p3 = 1 – 0,2 = 0,8.

P1 (X=0) = q1 ∙ q2 ∙ q3 = 0,95 ∙ 0,9 ∙ 0,8 = 0,684.

9.4. Функция двух случайных аргументов

Вероятности найденных возможных значений равны произведениям вероятностей

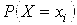
и

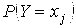
. Пример 10.6. Дискретные независимые случайные величины Х и Заданы распределениями: Х –2 –1 3 4 Р 0,3 0,1 0,5 0,1 Y 1 2 3 Р 0,4 0,1 0,5 Найти распределения случайных величин: а)

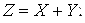
б)

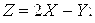
в)

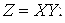
г)

.
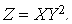